
Previously, we covered why automatic annotations are useful, and some basics underlying the infrastructure to perform automatic annotations.
In this post we’ll see how function types are inferred, as well as simple map types.
This work is part of a crowdfunding effort, please support the campaign here!

Automatic annotations for Typed Clojure only work if
you provide tests. Let’s suppose we have the following
point function with two unit tests.

As in the
previous post,
to track the value of a def you track its initial value.

Now we have an interesting problem: how do we track functions? We need to learn two things about functions, namely its inputs and output. By wrapping the original function, we can track each of these subcomponents.
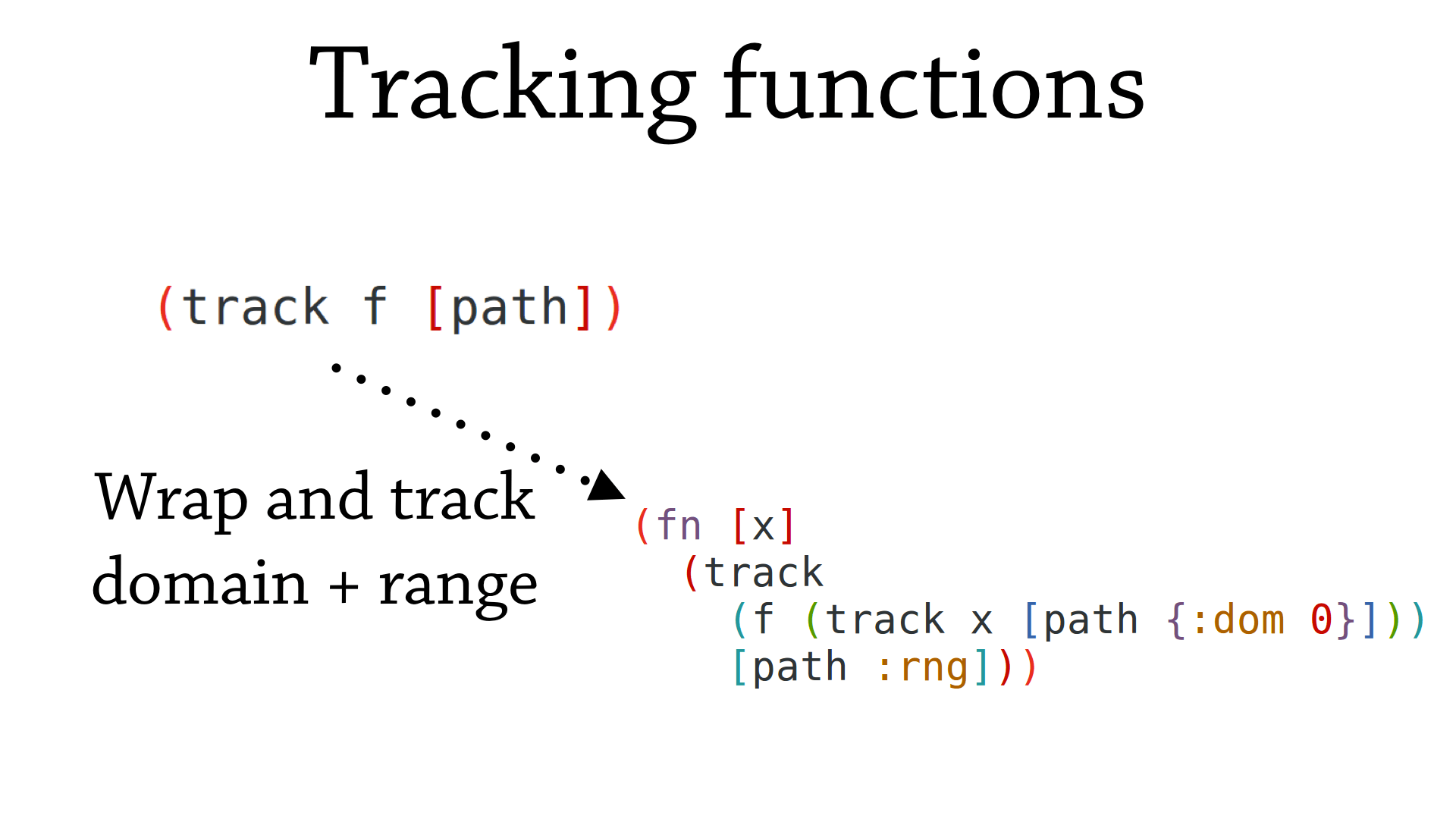
Since this waits for the function to be called, we need tests to exercise the function. This is the intuition behind Write Tests, Get Types!.
Let’s track point.

Notice we have added two new path elements corresponding to the input and output of functions. We can combine these to make arbitrarily deep paths, and encode statements like the first parameter’s second parameter of var foo-bar is of type Long.
Let’s step through the evaluation of (point 1 2).
First, the wrapped function is called and
we are left with a call to the original function.
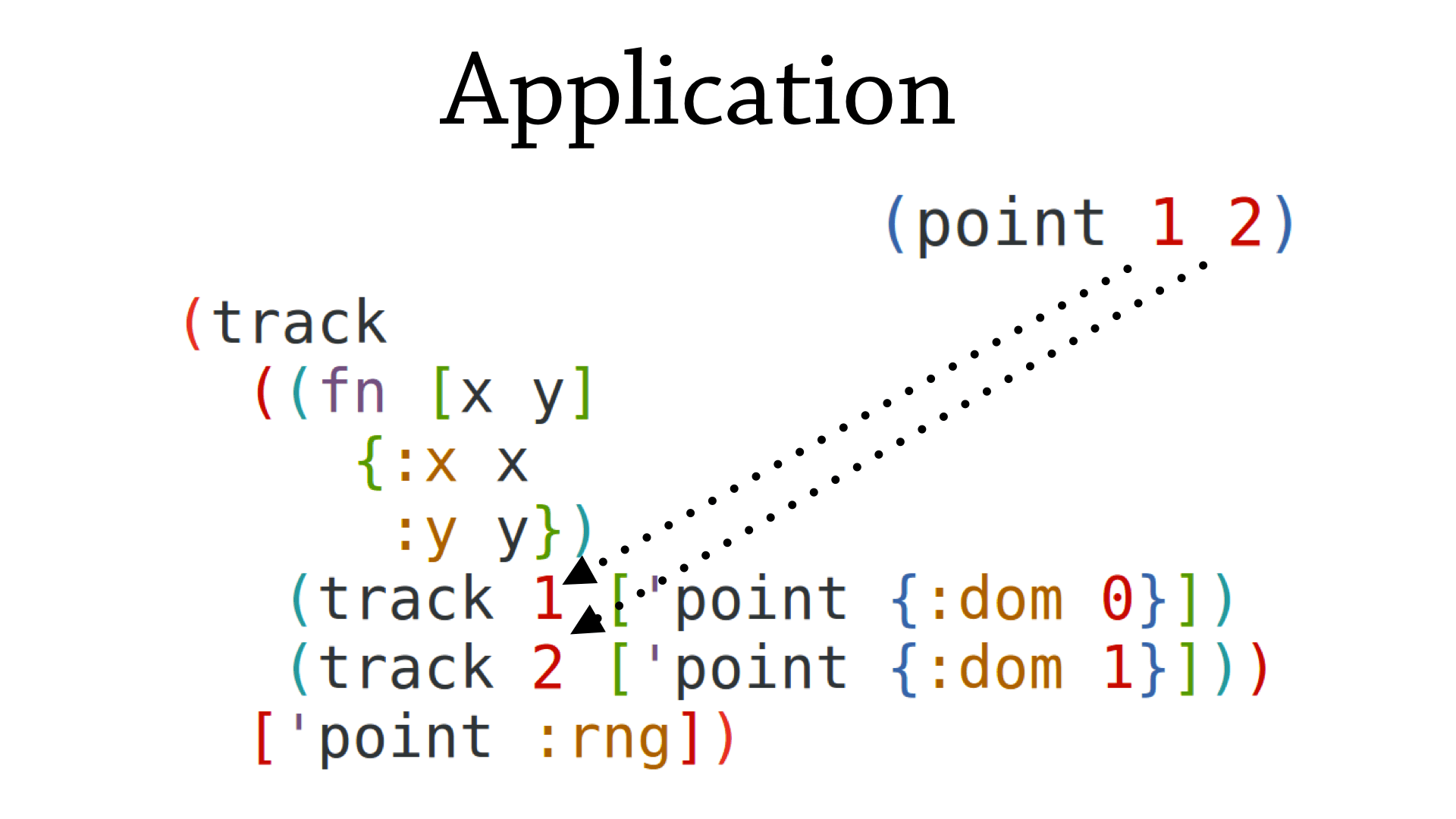
We then evaluate the first argument to point, which
tracks 1.

After this reduction, we infer the first argument to be
of type Long.
We then do the same for the second argument.

Now we have evaluated the arguments, we invoke the actual
point function.

It returns a map; to track a map, we need a new kind of
path element, key path elements, to track map entries.
We push the track inside the map’s values, using key path
elements.

Notice the richness of the paths here: 1 is point’s range’s
:x entry.
Reducing the first argument fills in part of the return type.

The final reduction completes the type of point.

Great, we have a type, but there is a mystery step we have
skipped: how we get from inference results like
[point (:dom 0)] : Long and [point (:dom 1)] : Long
to final var types like
point : [Long Long -> '{:x Long :y :Long}].
This is handled by converting inference results
to types, then combining then with join.
For example,
the type for point after inferring its arguments is
join([Long ? -> ?], [? Long -> ?]) = [Long Long -> ?]
Each new inference result is joined in this way, so inferring the function return type is similar.
Inferring Functions via Tests
The basic approach of inferring types for functions
is to wrap them and inspect their behaviour
when invoked.
The parameters and return types are incrementally
inferred, and combined with the join metafunction.
In the next post, we talk about inferring types for possibly-infinite sequences and vectors.
This work is part of a crowdfunding effort, please support the campaign here!