I am crowdfunding 12 months of full time development on Typed Clojure. Please pledge or share!

One of the first problems I attempted to solve with Typed Clojure turned out to be one of the most difficult: statically verifying Red/Black tree rebalancing invariants.

This post describes how close I am to checking these invariants. Note that the code examples might not be currently checkable.

I was lucky enough to have Rowan Davies supervise my Honours project on Typed Clojure. He introduced me to SML CIDRE, a refinement type checker for SML. Rowan’s perspective on types was an interesting counterpoint to mine, but perhaps even more interesting were the parallels between SML CIDRE and Typed Clojure: SML CIDRE is a type system layered on top of SML, and Typed Clojure is the same for Clojure.

The example that opened my eyes to the ability of SML CIDRE is one that checks a Red/Black tree implementation. SML CIDRE can statically verify the colour invariant of Red/Black tree rebalancing operations. This is quite remarkable.

Let’s explore the problem of verifying a Clojure Red/Black tree implementation with Typed Clojure.

An idiomatic Red/Black tree implementation in SML is defined using datatypes. In that spirit, the Clojure port will be implemented with plain hash maps.

Basic Types

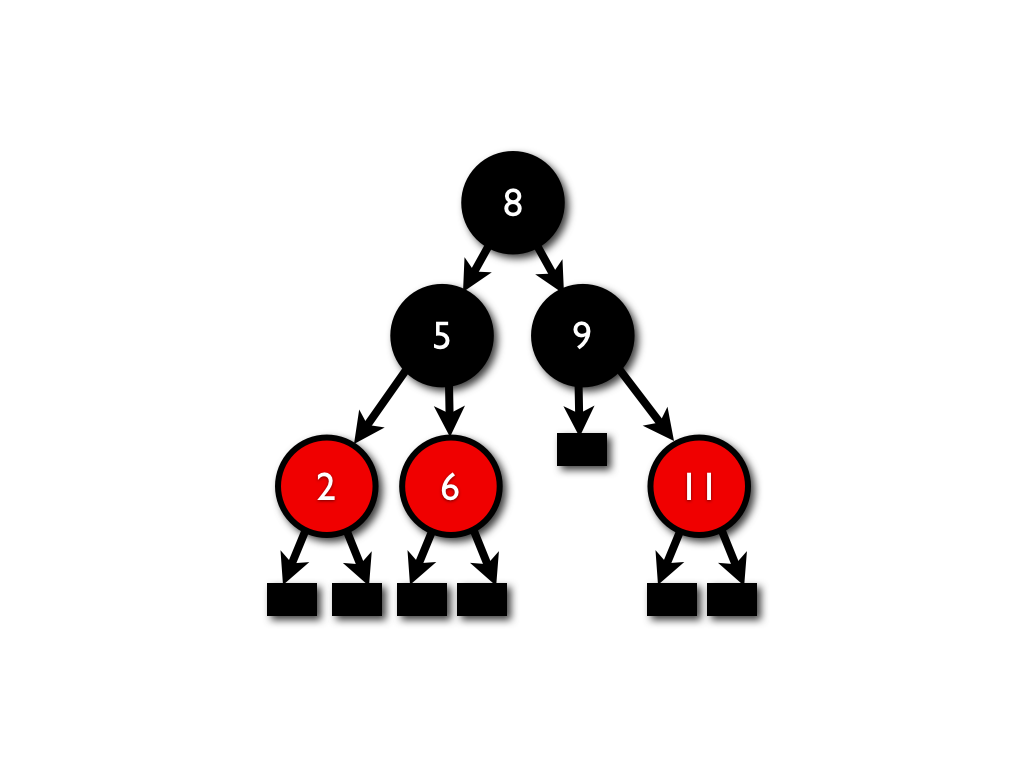
We need three basic types in a Red/Black tree implementation: Red nodes, Black nodes, and Leaf nodes.

In Typed Clojure, they are simply type aliases of heterogeneous maps, differentiated by the :tree entry.

(defalias EntryT 
  "The payload"
  '{:key Number
    :datum Number})

(defalias Empty
  "A terminating node."
  '{:tree ':Empty})

(defalias Red
  "A red node"
  (TFn [[l :variance :covariant]
        [r :variance :covariant]]
    '{:tree ':Red
      :entry EntryT
      :left l
      :right r}))

(defalias Black
  "A black node"
  (TFn [[l :variance :covariant]
        [r :variance :covariant]]
    '{:tree ':Black
      :entry EntryT
      :left l
      :right r}))

We also define EntryT, the payload type.

A refinement type in SML CIDRE is an additional layer of types over SML types for expressing logical properities and invariants. They are realised via datasorts (for example, search for ‘datasort’ in the Red/Black tree implementation). Refinement types are used to model and enforce the colour invariant of Red/Black trees by defining a set of type refinements, and then annotating the rebalancing functions with their expected types.

We can emulate something similar in Typed Clojure with heterogeneous maps, by taking advantage of subtyping between heterogeneous maps.

(defalias rbt 
  "Trees with only black children for red nodes"
  (U 
    Empty
    (Black rbt rbt)
    (Red bt bt)))

(defalias bt 
  "Like rbt but additionally the root node is black"
  (U 
    Empty
    (Black rbt rbt)))

(defalias red 
  "Trees with a red root"
  (Red bt bt))

(defalias badRoot 
  "Invariant possibly violated at the root"
  (U 
    Empty
    (Black rbt bt)
    (Red rbt bt)
    (Red bt rbt)))

(defalias badLeft 
  "Invariant possibly violated at the left child"
  (U
   Empty
   (Black rbt rbt)
   (Red bt bt)
   (Black badRoot rbt)))

(defalias badRight 
  "Invariant possibly violated at the right child"
  (U
   Empty
   (Black rbt rbt)
   (Red bt bt)
   (Black rbt badRoot)))

It is immediately interesting that these type aliases are not special as far as Typed Clojure types go. All of the types can be explained using unions (U) and heterogeneous maps.

Rebalancing operations

We can use our type aliases to annotate our rebalancing operators. For example, here is restore-right, that takes a badRight (a tree violated at the right child), and returns an rbt (a tree with only black children for red nodes).

(ann restore-right [badRight -> rbt])
(defn restore-right [tmap]
  (cond
    (and (= :Black (-> tmap :tree))
         (= :Red (-> tmap :left :tree))
         (= :Red (-> tmap :right :tree))
         (= :Red (-> tmap :right :left :tree)))
    (let [{lt :left rt :right e :entry} tmap]
      ;re-color
      {:tree :Red
       :entry e
       :left (assoc lt
                    :tree :Black)
       :right (assoc rt
                     :tree :Black)})

    (and (= :Black (-> tmap :tree))
         (= :Red (-> tmap :left :tree))
         (= :Red (-> tmap :right :tree))
         (= :Red (-> tmap :right :right :tree)))
    (let [{lt :left rt :right e :entry} tmap]
      {:tree :Red
       :entry e
       :left (assoc lt
                    :tree :Black)
       :right (assoc rt
                     :tree :Black)})

    (and (= :Black (-> tmap :tree))
         (= :Red (-> tmap :right :tree))
         (= :Red (-> tmap :right :left :tree)))
    (let [{e :entry
           l :left
           {re :entry
            {rle :entry
             rll :left
             rlr :right}
            :left
            rr :right}
           :right} tmap]
      ;l is black, deep rotate
      {:tree :Black
       :entry rle
       :left {:tree :Red
              :entry e
              :left l
              :right rll}
       :right {:tree :Red
               :entry re
               :left rlr
               :right rr}})

    (and (= :Black (-> tmap :tree))
         (= :Red (-> tmap :right :tree))
         (= :Red (-> tmap :right :right :tree)))
    (let [{e :entry
           l :left
           {re :entry
            rl :left
            rr :right} 
           :right} tmap]
      ;l is black, shallow rotate
      {:tree :Black
       :entry re
       :left {:tree :Red
              :entry e
              :left l
              :right rl}
       :right rr})

    :else tmap))

To check this implementation, Typed Clojure needs to understand the notion of a path down a map, and how to update it.

Typed Clojure needs to know that in the following branch

(if (= :Red (-> tmap :right :right :tree))
  e1
  e2)

it is recognised that

tmap has a :Red key down the path [:right :right :tree] when checking e1
tmap does not have a :Red key down the path [:right :right :tree] when checking e2

This style of updating works in Typed Clojure today.

The problem

What makes checking restore-right so difficult is the sheer number of types it must reason about. The rebalancing operators generate many type calculations, mainly type intersections. In fact, the most interesting aspect of this example is the huge number of intersection calculations with respect to the size of the code base (or any code base, for that matter).

To better understand the explosion of type calculations, let’s see what Typed Clojure infers from each branch.

The first branch isn’t horrible:

(and (= :Black (-> tmap :tree))
     (= :Red (-> tmap :left :tree))
     (= :Red (-> tmap :right :tree))
     (= :Red (-> tmap :right :left :tree)))

infers the proposition set:

{:then (& (is ':Black tmap [(Key :tree)])
          (is ':Red tmap [(Key :left) (Key :tree)])
          (is ':Red tmap [(Key :right) (Key :tree)])
          (is ':Red tmap [(Key :right) (Key :left) (Key :tree)]))
 :else (| (! ':Black tmap [(Key :tree)])
          (! ':Red tmap [(Key :left) (Key :tree)])
          (! ':Red tmap [(Key :right) (Key :tree)])
          (! ':Red tmap [(Key :right) (Key :left) (Key :tree)]))}

The :then entry states what is true in the then branch, and the :else branch states what is true in the else branch. It should be easy to guess what each proposition means by referring back to the original test expression.

For example, the expression

(= :Black (-> tmap :tree))

has the proposition set

{:then (is ':Black tmap [(Key :tree)])
 :else (! ':Black tmap [(Key :tree)])}

At the second branch, we’re starting to see a problem. Because we have to take the results of previous branches into account, we are inferring much more information:

(and (= :Black (-> tmap :tree))
     (= :Red (-> tmap :left :tree))
     (= :Red (-> tmap :right :tree))
     (= :Red (-> tmap :right :right :tree)))

infers the proposition set:

{:then
 (&
  (! (Value :Red) tmap [(Key :right) (Key :left) (Key :tree)])
  (is (Value :Red) tmap [(Key :right) (Key :tree)])
  (is (Value :Red) tmap [(Key :left) (Key :tree)])
  (is (Value :Black) tmap [(Key :tree)])
  (is (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])),
 :else
 (&
  (|
   (! (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)]))
  (|
   (! (Value :Red) tmap [(Key :right) (Key :left) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)])))}

If we go down the second then branch, this information will update tmap to:

(U Empty
   (Black rbt rbt)
   (Red bt bt)
   (Black rbt (Red bt rbt)))

Just for fun, here’s the 4th branch:

(and (= :Black (-> tmap :tree))
     (= :Red (-> tmap :left :tree))
     (= :Red (-> tmap :right :tree))
     (= :Red (-> tmap :right :right :tree)))

infers the proposition set:

{:then
 (&
  (|
   (! (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)]))
  (! (Value :Red) tmap [(Key :right) (Key :left) (Key :tree)])
  (is (Value :Red) tmap [(Key :right) (Key :tree)])
  (is (Value :Black) tmap [(Key :tree)])
  (is (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
  (|
   (! (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)]))),
 :else
 (&
  (|
   (! (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)]))
  (|
   (! (Value :Red) tmap [(Key :right) (Key :left) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)]))
  (|
   (! (Value :Red) tmap [(Key :right) (Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)]))
  (|
   (! (Value :Red) tmap [(Key :right) (Key :left) (Key :tree)])
   (! (Value :Red) tmap [(Key :right) (Key :tree)])
   (! (Value :Red) tmap [(Key :left) (Key :tree)])
   (! (Value :Black) tmap [(Key :tree)])))}

In the final clause, always returns the original tree, we should have refined the type of tmap to an rbt by taking into account all of the previous branches.

Solutions

SML CIDRE checks this Red/Black tree code in a matter of milliseconds. The checker precalculates all possible type intersections before type checking, which delivers massive performance improvements during checking.

Typed Clojure seems to choke under these intensive calculations.

To get this implementation to work, I suspect it involves:

tons of caching
aggressive simplification and rearrangement of types

Why?

While the Red/Black trees are fun, the most notable characteristic of the checking it is the sheer amount of types generated. We probably won’t be using this implementation in our own code.

If we can get this Red/Black tree implementation checking quickly and accurately there are several interesting results:

we can investigate whether it can check in Typed Racket
large conditionals with many branches will type check much faster, even in “normal” code
Typed Clojure could be a great way to further explore these kinds of problems

I am crowdfunding 12 months of full time development on Typed Clojure. If you want to see awesome problems like these solved in Typed Clojure, please pledge or share!

dissoc

Red/Black tree rebalancing invariants (with plain maps)

Basic Types

Refinement types

Rebalancing operations

The problem

Solutions

Why?